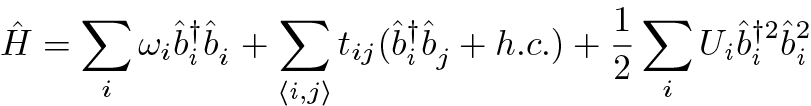This is a lite python library to generate the basis and many-body Hamiltonian for the Bose-Hubbard model.
The Bose-Hubbard model on some lattice is described by the Hamiltonian,
Here the sum runs over the lattice indices, and as is normal the operator b(i) annihilates a particle on site i.
This library requires numpy and scipy installed on your system.
As an example consider a ring with 8 sites.
Construct the model from a list of onsite-energies omegas, a list of links and hopping strengths, and the interaction energy U.
import bosehubbard
# The model parameters
omegas = [0]*8
links = [[i, (i+1) % 8, .1] for i in xrange(8)]
U = 2
# Construct the model
m = bosehubbard.Model(omegas, links, U)
# Look at the single-particle hopping hamiltonian
print(m.hopping)
# [[ 0. 0.1 0. 0. 0. 0. 0. 0.1]
# [ 0.1 0. 0.1 0. 0. 0. 0. 0. ]
# [ 0. 0.1 0. 0.1 0. 0. 0. 0. ]
# [ 0. 0. 0.1 0. 0.1 0. 0. 0. ]
# [ 0. 0. 0. 0.1 0. 0.1 0. 0. ]
# [ 0. 0. 0. 0. 0.1 0. 0.1 0. ]
# [ 0. 0. 0. 0. 0. 0.1 0. 0.1]
# [ 0.1 0. 0. 0. 0. 0. 0.1 0. ]]Because the Bose-Hubbard Hamiltonian commutes with the total number operator, we can investigate each particle number sector separately,
# Investigate the model with two bosons in it.
m2 = m.numbersector(2)
# Construct the many-body Hamiltonian (in sparse format)
H = m2.hamiltonian
print(H)
# ( 0, 0) 2.0
# ( 0, 1) 0.141421356237
# ( 0, 7) 0.141421356237
# ( 1, 0) 0.141421356237
# ( 1, 2) 0.1
# ( 1, 8) 0.141421356237
# ( 1, 14) 0.1
# : :
# (34, 6) 0.1
# (34, 32) 0.1
# (34, 33) 0.141421356237
# (34, 35) 0.141421356237
# (35, 7) 0.141421356237
# (35, 34) 0.141421356237
# (35, 35) 2.0One can access the many-body basis in the two boson sector by looking at the Basis object,
basis = m2.basis
print(basis.vs)
# [[2 0 0 0 0 0 0 0]
# [1 1 0 0 0 0 0 0]
# [1 0 1 0 0 0 0 0]
# [1 0 0 1 0 0 0 0]
# [1 0 0 0 1 0 0 0]
# [1 0 0 0 0 1 0 0]
# [1 0 0 0 0 0 1 0]
# [1 0 0 0 0 0 0 1]
# [0 2 0 0 0 0 0 0]
# ...
# [0 0 0 0 0 0 1 1]
# [0 0 0 0 0 0 0 2]]