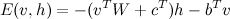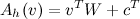RBMs in Morb

Units and parameters

In Morb, an RBM is defined by specifying a set of units and a set of parameters. The units represent the random variables that are being modelled. In an RBM, some of these will be observed and some will be latent, but this distinction is not made when it is not necessary (in practice: only during training). The parameters define relations between the units, by specifying potentials that are added to the energy function of the RBM. Potentials that are high (low) for a particular configuration of units will increase (decrease) the energy of this configuration, and thus make it less likely.

Units are represented by instances of the Units class. Different types of units correspond to different subclasses of Units. Essentially, a type of units defines two things:

• the domain of the values that these units can assume (discrete, continuous on [0, 1], continuous and positive, ...)
• the distribution across this domain (bernoulli, gaussian, exponential, ...)

In fact, a units type is nothing more than a sampler for a particular distribution. In practice, a Units subclass implements at least a sample method, and optionally also a mean_field method, which gives the mean of the distribution, and a free_energy_term method which specifies what the term corresponding to these units in the free energy looks like, when they are integrated out.

Parameters / potentials are represented by instances of the Parameters class. Different types of potentials correspond to different subclasses of Parameters. A type of parameters defines:

• a parametrised contribution to the energy function of the RBM (energy_term)
• its gradient w.r.t. each of the parameters (energy_gradient)
• the term it contributes to the 'activation' of each of the Units instances whose values the energy term depends on (terms)

Activations

The activation of a Units instance is defined as the negative of its 'cofactor' in the energy function. For example, the typical RBM with visible units v and hidden units h has an energy function of the form:

We can write this as:

Which makes it clear that the activation of h is:

Activations are important, because the distribution of a given set of units can typically be expressed in terms of its activation (which of course depends on the values of the other units). This is true if all energy potentials are linear in the unit values.

Dealing with non-linear potentials

TODO: non-linear