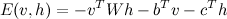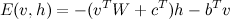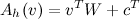RBMs in Morb

RBMs in Morb

Units and parameters

In Morb, an RBM is defined by specifying a set of units and a set of parameters. The units represent the random variables that are being modelled. In an RBM, some of these will be observed and some will be latent, but this distinction is not made when it is not necessary (in practice: only during training). The parameters define relations between the units, by specifying potentials that are added to the energy function of the RBM. Potentials that are high (low) for a particular configuration of units will increase (decrease) the energy of this configuration, and thus make it less (more) likely.

Units are represented by instances of the Units class. Different types of units correspond to different subclasses of Units. Essentially, a type of units defines two things:

• the domain of the values that these units can assume (discrete, continuous, continuous and positive, continuous on [0, 1], ...)
• the distribution across this domain (bernoulli, gaussian, exponential, truncated exponential, ...)

In fact, a units type is nothing more than a sampler for a particular distribution. In practice, a Units subclass implements at least a sample method, and optionally also a mean_field method, which gives the mean of the distribution, and a free_energy_term method which specifies what the term corresponding to these units in the free energy looks like, when they are integrated out.

Parameters / potentials are represented by instances of the Parameters class. Different types of potentials correspond to different subclasses of Parameters. A type of parameters defines:

• a parameterised contribution to the energy function of the RBM (energy_term)
• its gradient w.r.t. each of the parameters (energy_gradient)
• the term it contributes to the 'activation' of each of the Units instances whose values the energy term depends on (terms)

Activations

The activation of a Units instance is defined as minus its 'cofactor' in the energy function. For example, the typical RBM with visible units v and hidden units h has an energy function of the form:

We can write this as:

Which makes it clear that the activation of h is:

Activations are important, because the parameters of the distribution of a given set of units can be expressed in terms of their activation (which of course depends on the values of the other units). This is true if all energy potentials are linear in the unit values. For example, for bernoulli units, the mean parameter is equal to the sigmoid of the activation. For gaussian units with fixed variance, the mean parameter is equal to the activation.

Dealing with non-linear potentials

When non-linear functions of the unit values occur in the energy potentials, this definition of 'activation' is ambiguous. However, we can deal with non-linear potentials by first 'linearising' them.

To do this, we replace every function of the unit values by a new set of 'proxy units'. For example, let's say we have the following energy function:

We define a new set of proxy units . We can then write the energy function like this:

It is important to realise that x and v are not independent, but because their relationship is deterministic, this doesn't cause any huge problems. It becomes important, however, to ensure that 'consistent' samples are drawn from x and v during RBM training. This is easily achieved by sampling v and then computing x from the sampled values.

The distribution of v can now be expressed in terms of the activations of all of its proxies and itself (in this case: and ).

Variable maps

Many methods require a vmap or variable map as input. This is simply a Python dictionary that maps Units instances to Theano variables or expressions. These are used rather than positional function arguments, because Morb is designed to handle an arbitrary number of units instances.

Training

'Training' an RBM is updating the parameters in order to optimise some objective function. For RBMs, 'contrastive divergence' and its variants are a popular choice. Since the objective function typically isn't convex, it is optimised iteratively, by repeatedly updating the parameters.

Update rules for parameters are specified using Updaters. An updater computes some kind of contribution to the update term. Updaters are compositional: adding two Updater instances together yields a new instance that represents the sum of the updates. Instances can also be multiplied by scalars (this is how learning rates and regularisation parameters are implemented). Updater instances can also encapsulate other instances (this is how the MomentumUpdater works, for example).

There are Updater subclasses for sparsity regularisation, momentum, weight decay and for the contrastive divergence learning rule. The latter requires some statistics obtained from training data. These are provided by a Stats instance. For example, in a typical binary-binary RBM trained with CD-k, the needed statistics are the values of the visibles and hiddens at step 0 (data phase or positive phase) and their values at step k (model phase or negative phase).

To perform the actual parameter updates, the update rules need to be compiled into a training function. This is done using a Trainer instance.

Parameter tying

Morb supports parameter tying transparently: by reusing the same Theano variable multiple times. The different gradient terms for these parameter values will automatically be summed where applicable.