README.md

814. 二叉树剪枝

English Version

题目描述

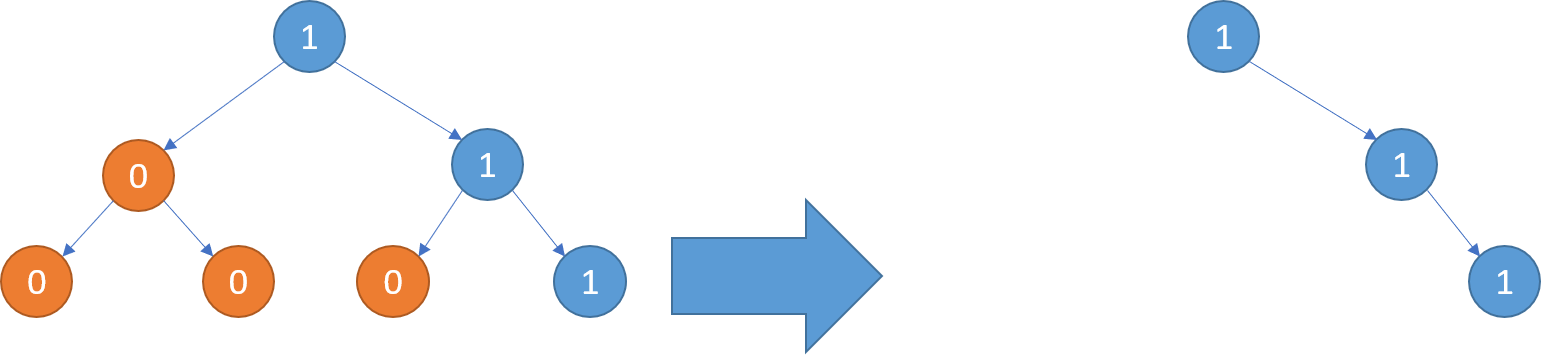
给定二叉树根结点 root ，此外树的每个结点的值要么是 0，要么是 1。

返回移除了所有不包含 1 的子树的原二叉树。

( 节点 X 的子树为 X 本身，以及所有 X 的后代。)

示例1:
输入: [1,null,0,0,1]
输出: [1,null,0,null,1]

解释:
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案。

示例2:
输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]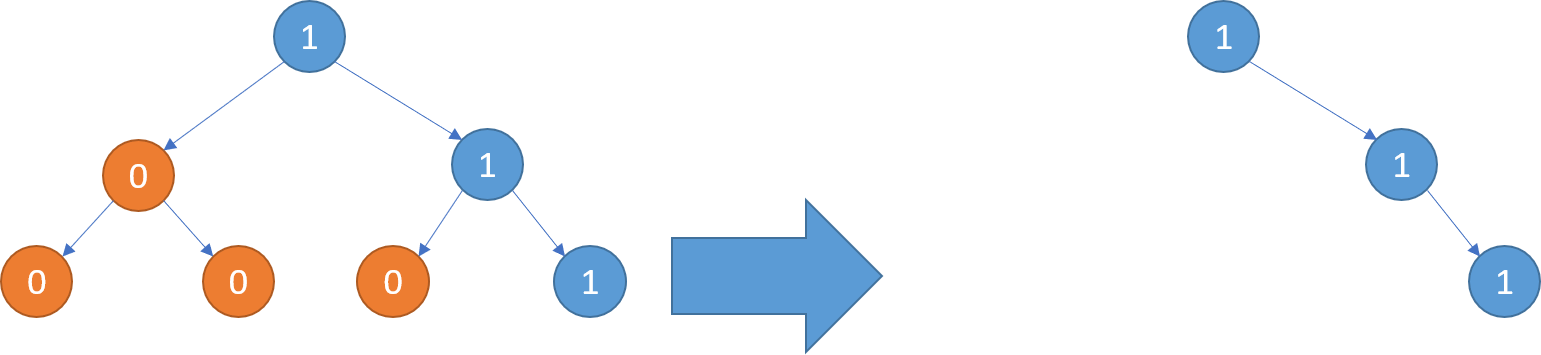

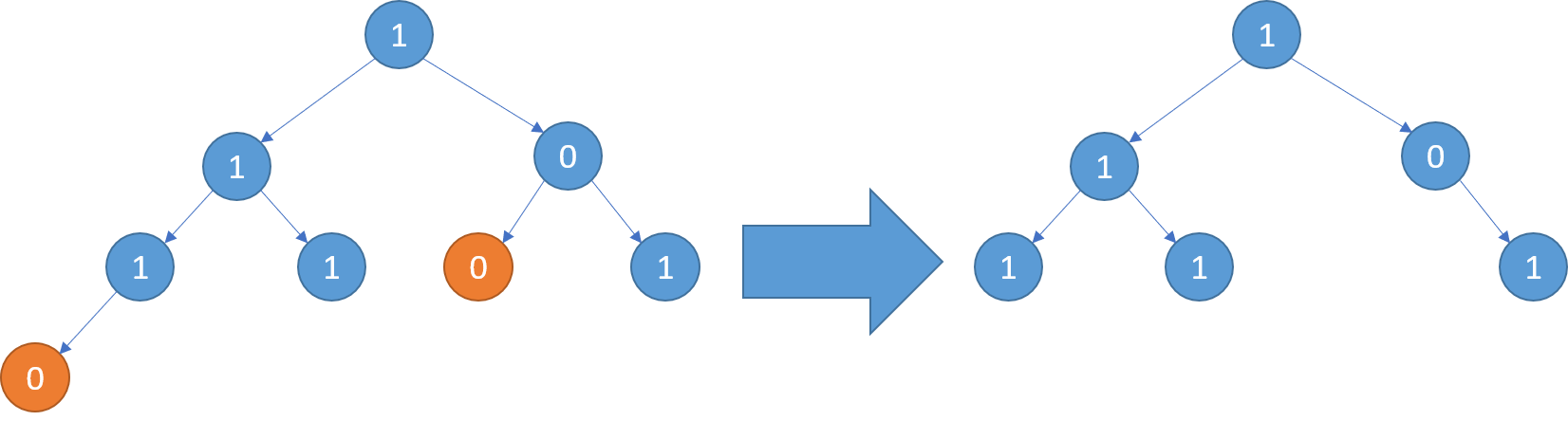
示例3:
输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]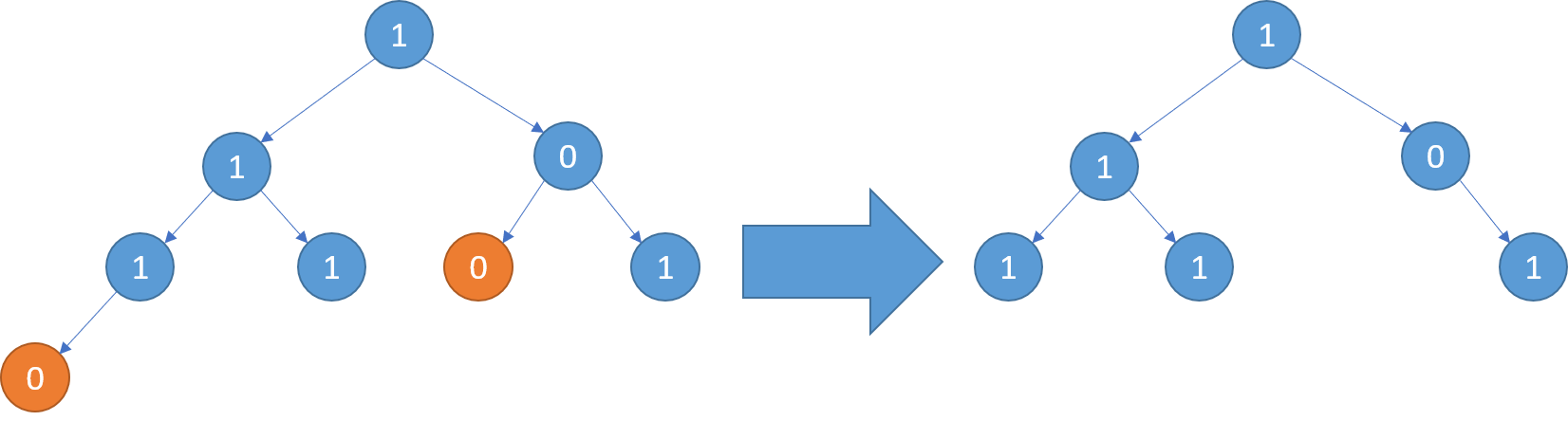

说明:

• 给定的二叉树最多有 100 个节点。
• 每个节点的值只会为 0 或 1 。

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pruneTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        root.left = self.pruneTree(root.left)
        root.right = self.pruneTree(root.right)
        if root.val == 0 and not root.left and not root.right:
            return None
        return root

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode pruneTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        root.left = pruneTree(root.left);
        root.right = pruneTree(root.right);
        if (root.val == 0 && root.left == null && root.right == null) {
            return null;
        }
        return root;
    }
}

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func pruneTree(root *TreeNode) *TreeNode {
	if root == nil {
		return nil
	}
	root.Left = pruneTree(root.Left)
	root.Right = pruneTree(root.Right)
	if root.Val == 0 && root.Left == nil && root.Right == nil {
		return nil
	}
	return root
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if (!root) return nullptr;
        root->left = pruneTree(root->left);
        root->right = pruneTree(root->right);
        if (!root->val && !root->left && !root->right) return nullptr;
        return root;
    }
};

...