#数据结构 #算法 #C
子串的定位操作通常称为串的模式匹配,它求的是子串(常称模式串 Pattern String)在主串中的位置。即在主串(被搜索的串)中找到与模式串(需要寻找的目标串)相同的⼦串,并返回其所在位置。
通常最容易想到的方法,就是使用暴力求解。
以下以主串⻓度为 N,模式串⻓度为 M 为例子,进行一种暴力匹配示例。
将长度为N主串中所有⻓度为M的⼦串依次与模式串对⽐,直到找到⼀个完全匹配的⼦串,或所有的⼦串都不匹配为⽌。这一过程,最多对⽐ N - M + 1 个⼦串。这种算法即称为朴素模式匹配算法(BruteForce) 。
串中的函数Index(S, T)即是模式匹配算法的实现。
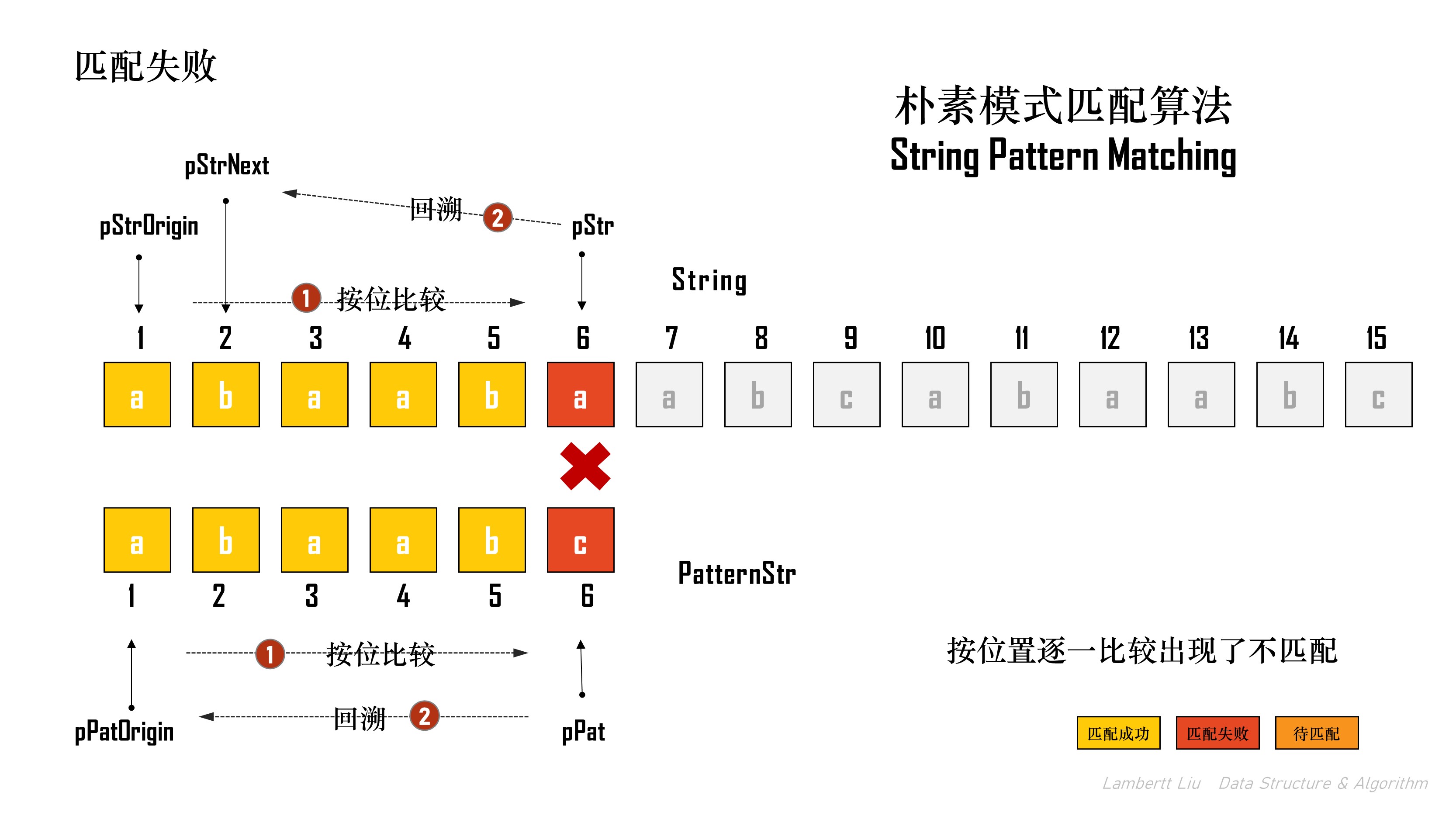
以下,不使⽤字符串的基本操作,直接通过数组下标实现朴素模式匹配算法。 具体分中间过程的匹配失败:
- 当指针小于主串和模式串字符串长度,启动逐个字符匹配
- 如果有字符相等,继续比较后续字符串
- 一旦出现字符不相等,匹配失败,主串指针
pStr指向起初匹配⼦串的第⼀个位置的次一个,模式串指针pPat回到模式串的第⼀个位置,在这个基础上继续进行逐个字符匹配 - 完成退出循环时,比较模式串的指针的位置,确定匹配结果。
和匹配成功:
int Index (StaticString S, StaticString T)
{
// 设置两个扫描指针,分别指向主串 String 和模式串 Pattern
int pStr = 1, pPat = 1;
// 必须满足指针小于字符串长度,否则比较无意义。
while (pStr <= S.length && pPat <= T.length) {
// 如果有字符相等,继续比较后续字符串
if (S.ch[pStr] == T.ch[pPat]) {
++pStr;
++pPat;
/* 一旦出现字符不相等,匹配失败
主串指针 pStr 指向下⼀个⼦串的第⼀个位置,
模式串指针 pPat 回到模式串的第⼀个位置, 指针后退重新开始匹配
*/
} else {
pStr = pStr - pPat + 2;
pPat = 1;
}
}
/* 退出循环的时候可能是有以下情况:
1. pStr > S.length, S已经完全扫描完, 遍历结束也没有匹配
2. pPat > T.length, T已经完全扫描完, S还未完全遍历已匹配
对于情况1 和2, 需要判定究竟是哪一类
对 pPat 的值进行检验 ( 对s的值检验无效,是否匹配均有可能 )
*/
if (pPat > T.length) {
return pStr - T.length;
} else {
return 0;
}
}设主串⻓度为
最坏时间复杂度 =
最好时间复杂度 =
推导:
-
最坏的情况:
每个子串都要对比$M$ 个字符,共$N - M + 1$ 个子串,
复杂度 =$O((N - M + 1) * M)$ =$O(N*M)$
因为,很多时候,$N >> M$ -
最好的情况:
每个⼦串的第⼀个字符就匹配失败,共$N - M + 1$ 个⼦串
复杂度 =$O(N - M + 1)$ =$O(N)$
由D.E.Knuth,J.H.Morris和V.R.Pratt提出,因此取三个人姓名首字母称为 KMP算法,该算法对朴素模式匹配算法优化而得。
论文参考链接:FAST PATTERN MATCHING IN STRINGS_1977.pdf (ufpe.br)
【预先结论】
已知模式串 T,S , 循环中,遍历串字符,当第i(i > 1)个元素匹配失败时,第 i 个元素之前的元素是已经匹配成功的。
【问题】
那么以模式串abaabc为例,在匹配到第六个元素出现失败的时候,是否需要把主串指针和模式串指针回溯到初始位置呢?
【结论】
其实是不需要的,对于KMP算法而言,这些已经匹配成功的字符将会被直接舍去。
因为在已知前5个元素的位置的时候,再回溯到初始位置匹配的时候,一定是会匹配失败的,可以直接指定到主串指针不变,而模式串指针直接定位到 pPat = 3,以这里为起点再进行匹配。
对于已知模式串 T = 'abaabc',主串的元素是未知的。对适配情况进行列举:
- 当 第6个元素匹配失败时,可令主串指针
pStr不变,模式串指针pPat = 3;
- 当 第5个元素匹配失败时,可令主串指针
pStr不变,模式串指针pPat = 2;
- 当 第4个元素匹配失败时,可令主串指针
pStr不变,模式串指针pPat = 2;
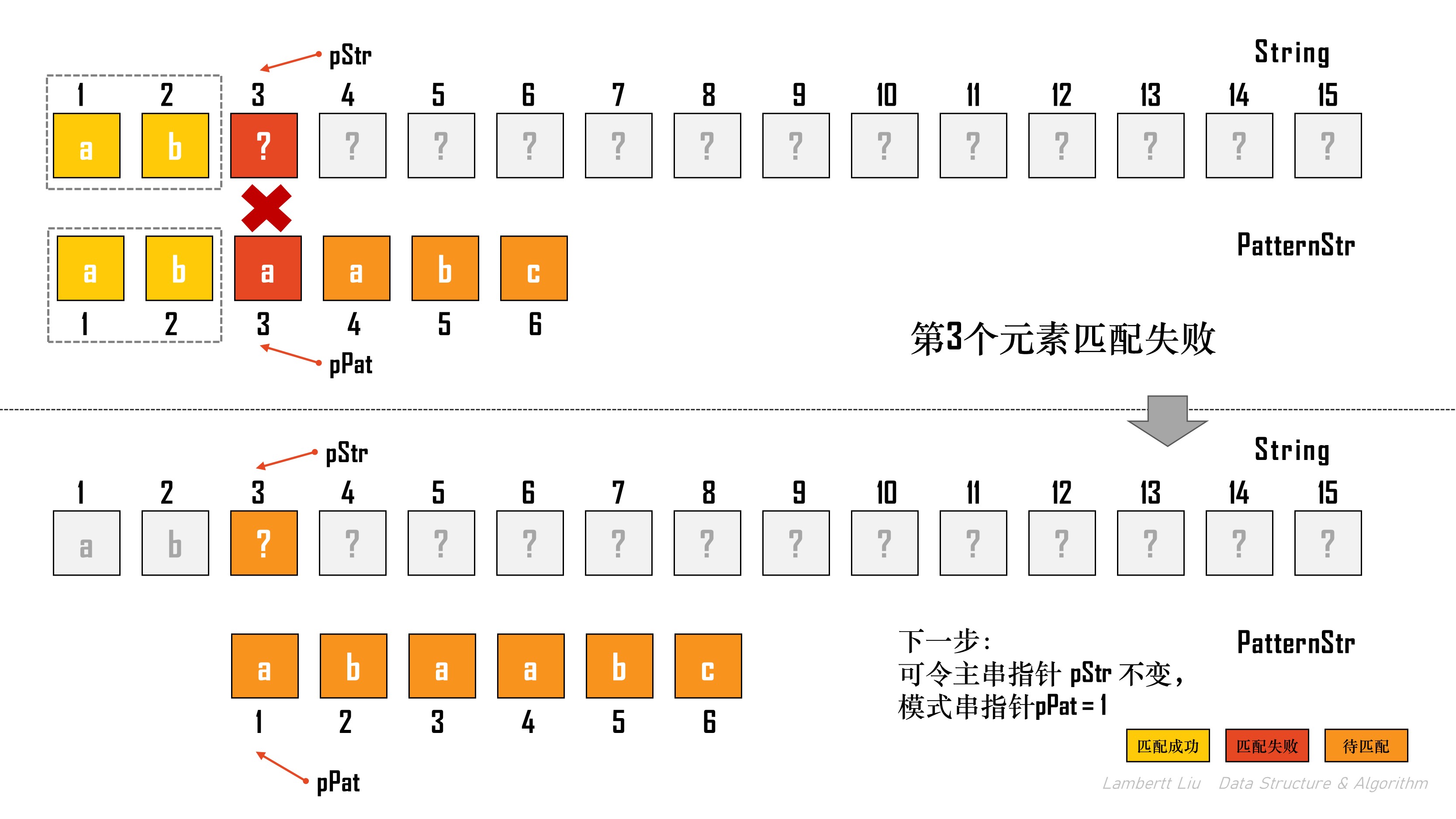
- 当 第3个元素匹配失败时,可令主串指针
pStr不变,模式串指针pPat = 1;
- 当 第2个元素匹配失败时,可令主串指针
pStr不变,模式串指针pPat = 1;
- 当 第1个元素匹配失败时,匹配下⼀个相邻⼦串,令
pPat = 0, pStr++, pPat++;。
下面以主串S = "abaabaabcabaabc",模式串T="abaabc"为例。使用优化后的模式匹配算法进行字符串匹配:
与朴素模式匹配算法相比,在进行匹配过程中,主串指针不回溯。
下一步,如何确定匹配过程失败时候,主串指针的位置?
解决方式:利用穷举方式,将主串匹配失败pStr位置与模式串指针pPat位置建立数组。称之为next数组。
next[0] |
next[1] |
next[2] |
next[3] |
next[4] |
next[5] |
next[6] |
|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 2 | 2 | 3 |
next数组表示,当匹配失败过程时,主串pStr指针不回溯,next数组指明j指针的下个位置。next数组只和短的模式串有关,和长的主串无关。
总结:
KMP算法,根据模式串T,求出 next 数组,利⽤next数组进⾏匹配,当匹配失败过程时,主串pStr指针不回溯,next数组指明j指针的下个位置。
// KMP算法实现
int Index_KMP(StaticString S, StaticString T, int next[]){
int pStr = 1, pPat = 1;
while(pStr <= S.length && pPat <= T.length){
if (pPat == 0 || S.ch[pStr] == T.ch[pPat]){
++pStr;
++pPat; // 继续比较后继字符
} else {
pPat = next[pPat]; // 模式串向右移动
}
}
if (pPat > T.length){
return pStr - T.length;
} else {
return 0;
}
}最坏时间复杂度
其中,求 next 数组时间复杂度
模式匹配过程最坏时间复杂度
根据模式串T,求出 next 数组。
next数组的作⽤:当模式串的第 j 个字符失配时,从模式串的第 next[j] 的继续往后匹配。
【问题】
以模式串"google"为例,以穷举法,求该模式串next数组具体值。
任何模式串都⼀样,第1个字符不匹配时,只能匹配下⼀个⼦串,因此,往后,next[1]都⽆脑写 0。然后再继续执行以下程序:
if (j == 0) {
i++;
j++; }任何模式串都⼀样,第2个字符不匹配时,应尝试匹配模式串的第1个字符,因此,往后,next[2]都⽆脑写 1。
在不匹配的位置前边,划⼀根分界线,模式串⼀步⼀步往后退,直到分界线之前“能对上”,或模式串完全跨过分界线为⽌。 此时 pPat 指向哪⼉,next数组值就是多少。
对于模式串"google",next[3] = 1。
在不匹配的位置前边,划⼀根分界线,模式串⼀步⼀步往后退,直到分界线之前“能对上”,或模式串完全跨过分界线为⽌。 此时 pPat 指向哪⼉,next数组值就是多少。
对于模式串"google",next[4] = 1。
在不匹配的位置前边,划⼀根分界线,模式串⼀步⼀步往后退,直到分界线之前“能对上”,或模式串完全跨过分界线为⽌。 此时 pPat 指向哪⼉,next数组值就是多少。
对于模式串"google",next[5] = 2,因为当模式串移动至第1个元素在分界线左边的时候,可以和主串对应上,可能出现匹配情况。
在不匹配的位置前边,划⼀根分界线,模式串⼀步⼀步往后退,直到分界线之前“能对上”,或模式串完全跨过分界线为⽌。 此时 pPat 指向哪⼉,next数组值就是多少。
对于模式串"google",next[6] = 1。
next[1] = 0 ,next[2] = 1.
其他 next[i]:在不匹配的位置前,划⼀根分界线;模式串⼀步⼀步往后退,直到分界线之前“能对上”,或模式串完全跨过分界线为止。此时 pPat 指向哪⼉,next数组值就是多少。
next数组的实质是关于字符串的部分匹配表(PMT表)。
以字符串'abababca'为例,它的PMT表格:
| Char | a | b | a | b | a | b | c | a |
|---|---|---|---|---|---|---|---|---|
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Value | 0 | 0 | 1 | 2 | 3 | 4 | 1 | 2 |
深入了解KMP算法 PMT表,就必须离不开对字符串的引申属性前缀、后缀进行介绍:
【前缀 prefix】
如果字符串
'Harry'的前缀包括 {'H', 'Ha', 'Har', 'Harr'} ,我们把所有前缀组成的集合,称为字符串的前缀集合。
【后缀 suffix】
同样可以定义后缀 'Potter'的后缀包括 {'otter', 'tter', 'ter', 'er', 'r'} ,然后把所有后缀组成的集合,称为字符串的后缀集合。
要注意的是,字符串本身并不是自己的后缀。
【部分匹配表】
部分匹配表 (Partial Match Table, PMT) 中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
对于'aba',它的前缀集合为{'a', 'ab'},后缀 集合为{'ba', 'a'}。两个集合的交集为{'a'},那么长度最长的元素就是字符串'a'了,长度为1,所以对于'aba'而言,它在PMT表中对应的值就是1。
对于字符串'ababa',它的前缀集合为{'a', 'ab', 'aba', 'abab'},它的后缀集合为{'baba', 'aba', 'ba', 'a'}, 两个集合的交集为{'a', 'aba'},其中最长的元素为'aba',长度为3。所以对于'ababa'而言,它在PMT表中对应的值就是3。
以在主串"ababababca"中查找模式字符串"abababca"为例子。
当主串和模式串在 j 处字符不匹配,那么由于前边所说的模式字符串 PMT 的性质(前缀集合与后缀集合的交集中最长元素的长度),主字符串中i指针之前的 PMT[j − 1] 位就一定与模式字符串的第 0 位至第 PMT[j − 1] 位是相同的。
证明如下:
- 因为主字符串在
i位失配,也就意味着主字符串从i − j到i这一段是与模式字符串的0到j这一段是完全相同的(匹配失败前的若干已经匹配位必然一致)。 - 根据模式串的PMT属性,模式字符串从
0到j − 1,在这个例子中就是'ababab',其前缀集合与后缀集合的交集的最长元素为'abab', 长度为4。 - 可以断言,主字符串中
i指针之前的 4 位一定与模式字符串的第0位至第 4 位是相同的,即长度为 4 的后缀与前缀相同。 - 所以,我们就可以将这些字符段的比较省略掉。具体的做法是,保持
i指针不动,然后将j指针指向模式字符串的PMT[j − 1]位即可。 而这一步,跳过的步骤,即是KMP算法的过程步骤。
有了上面的思路,我们就可以使用PMT加速字符串的查找了。
我们看到如果是在 j 位失配,那么影响 j 指针回溯的位置的其实是第 j − 1 位的 PMT 值。
所以为了编程的方便, 我们不直接使用PMT数组,而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。
KMP算法,即是根据next数组进行字符串匹配加速的字符串匹配程序。其中要注意的一个技巧是,在把PMT进行向右偏移时,第0位的值,我们将其设成了-1,这只是为了编程的方便,并没有其他的意义。在本节的例子中,next数组如下表所示。
| Char | a | b | a | b | a | b | c | a |
|---|---|---|---|---|---|---|---|---|
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Value | 0 | 0 | 1 | 2 | 3 | 4 | 0 | 1 |
| next | -1 | 0 | 0 | 1 | 2 | 3 | 4 | 0 |
程序实现:
int KMP(char * t, char * p)
{
int i = 0;
int j = 0;
while (i < (int)strlen(t) && j < (int)strlen(p))
{
if (j == -1 || t[i] == p[j])
{
i++;
j++;
} else {
j = next[j];
}
}
if (j == strlen(p))
return i - j;
else
return -1;
}这里的下标索引统一按照从0开始的数组表示方法,而前三节的规则以位序为索引,二者相差1,因此,与上文中的程序不同,next数组的顺序也顺位移动1位。
再看一下如何编程快速求得next数组,依然以'abababca'为例子。
其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前位置的next值。如下图所示:
程序实现:
void getNext(char *p, int *next)
{
next[0] = -1;
int i = 0, j = -1;
while (i < (int)strlen(p))
{
if (j == -1 || p[i] == p[j])
{
++i;
++j;
next[i] = j;
}
else
j = next[j];
}
}